Spin-Echo and Solid-Echo¶

In [6]:

from tins import spinsys, mesolve, mesolve_single
from scipy.linalg import expm
import numpy as np
import matplotlib.pyplot as plt

np.set_printoptions(precision=2, suppress=True)

from tins import spinsys, mesolve, mesolve_single from scipy.linalg import expm import numpy as np import matplotlib.pyplot as plt np.set_printoptions(precision=2, suppress=True)

In [7]:

import pulseplot as pplot
fig, ax = pplot.subplots(ncols=2, figsize=(6, 1), constrained_layout=True)

ax[0].pseq(r"""
p5 sp=fid wait ecr
d10 tx=$\tau$ tdy=0.1
p1 ph_180$_x$ fck pdy0.1
d10 tx=$\tau$ tdy=0.1
p5 sp=fid wait ecr
p-5 sp=fid ecr
""")
ax[0].draw_channels(0.45)

ax[1].pseq(r"""
p5 sp=fid wait ecr
d10 tx=$\tau$ tdy=0.1
p1 ph_90$_y$ fck pdy0.1
d10 tx=$\tau$ tdy=0.1
p5 sp=fid wait ecr
p-5 sp=fid ecr
""")
ax[1].draw_channels(0.45)

import pulseplot as pplot fig, ax = pplot.subplots(ncols=2, figsize=(6, 1), constrained_layout=True) ax[0].pseq(r""" p5 sp=fid wait ecr d10 tx=$\tau$ tdy=0.1 p1 ph_180$_x$ fck pdy0.1 d10 tx=$\tau$ tdy=0.1 p5 sp=fid wait ecr p-5 sp=fid ecr """) ax[0].draw_channels(0.45) ax[1].pseq(r""" p5 sp=fid wait ecr d10 tx=$\tau$ tdy=0.1 p1 ph_90$_y$ fck pdy0.1 d10 tx=$\tau$ tdy=0.1 p5 sp=fid wait ecr p-5 sp=fid ecr """) ax[1].draw_channels(0.45)

In [8]:

I = spinsys(0.5)

I = spinsys(0.5)

In [22]:

out = mesolve(
    start=I.x, 
    detect=I.p,
    ham=2 * np.pi * 20 * I.z, 
    time=np.linspace(0, 1, 1000)
)

out = mesolve( start=I.x, detect=I.p, ham=2 * np.pi * 20 * I.z, time=np.linspace(0, 1, 1000) )

In [24]:

fig, ax = plt.subplots(figsize=(6, 2))
ax.plot(out.real)
plt.show()

fig, ax = plt.subplots(figsize=(6, 2)) ax.plot(out.real) plt.show()

In [ ]:

def spinecho(cs):
    out_1 = mesolve(
            start=I.x, 
            detect=None, 
            ham=2 * np.pi * cs * I.z, 
            time=np.linspace(0, 0.5e-3, 60)
        )

    out_2 = mesolve(
            start=out_1[-1], 
            detect=None, 
            ham=2 * np.pi * 10000 * I.x, 
            time=np.linspace(0, 50e-6, 6)
        )

    out_3 = mesolve(
            start=out_2[-1], 
            detect=None, 
            ham=2 * np.pi * cs * I.z, 
            time=np.linspace(0, 0.5e-3, 60)
        )
    
    
    out = np.vstack((out_1, out_2, out_3))

    return out

def spinecho(cs): out_1 = mesolve( start=I.x, detect=None, ham=2 * np.pi * cs * I.z, time=np.linspace(0, 0.5e-3, 60) ) out_2 = mesolve( start=out_1[-1], detect=None, ham=2 * np.pi * 10000 * I.x, time=np.linspace(0, 50e-6, 6) ) out_3 = mesolve( start=out_2[-1], detect=None, ham=2 * np.pi * cs * I.z, time=np.linspace(0, 0.5e-3, 60) ) out = np.vstack((out_1, out_2, out_3)) return out

In [ ]:

def spinecho_ni(cs):
    out_1 = mesolve(
            start=I.x, 
            detect=None, 
            ham=2 * np.pi * cs * I.z, 
            time=np.linspace(0, 0.5e-3, 60)
        )

    out_2 = mesolve(
            start=out_1[-1], 
            detect=None, 
            ham=2 * np.pi * 1000 * I.x + 2 * np.pi * cs * I.z, 
            time=np.linspace(0, 500e-6, 6)
        )

    out_3 = mesolve(
            start=out_2[-1], 
            detect=None, 
            ham=2 * np.pi * cs * I.z, 
            time=np.linspace(0, 0.5e-3, 60)
        )
    
    out = np.zeros(out_1.shape[0] + out_2.shape[0] + out_3.shape[0])

    out = np.vstack((out_1, out_2, out_3))

    return out

def spinecho_ni(cs): out_1 = mesolve( start=I.x, detect=None, ham=2 * np.pi * cs * I.z, time=np.linspace(0, 0.5e-3, 60) ) out_2 = mesolve( start=out_1[-1], detect=None, ham=2 * np.pi * 1000 * I.x + 2 * np.pi * cs * I.z, time=np.linspace(0, 500e-6, 6) ) out_3 = mesolve( start=out_2[-1], detect=None, ham=2 * np.pi * cs * I.z, time=np.linspace(0, 0.5e-3, 60) ) out = np.zeros(out_1.shape[0] + out_2.shape[0] + out_3.shape[0]) out = np.vstack((out_1, out_2, out_3)) return out

In [9]:

se = [spinecho(i) for i in range(-300, 300, 50)]
se_ni = [spinecho_ni(i) for i in range(-300, 300, 50)]

se = [spinecho(i) for i in range(-300, 300, 50)] se_ni = [spinecho_ni(i) for i in range(-300, 300, 50)]

In [10]:

from tins import bloch_animation

from tins import bloch_animation

In [11]:

%%capture
bloch_animation(se, spin=I, outfile='spinecho.gif')

%%capture bloch_animation(se, spin=I, outfile='spinecho.gif')

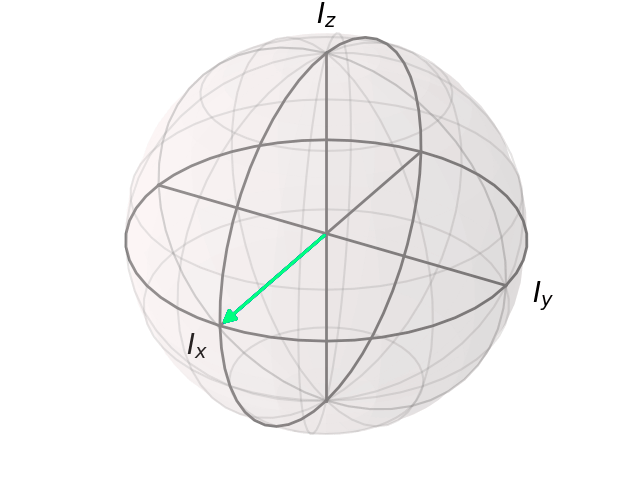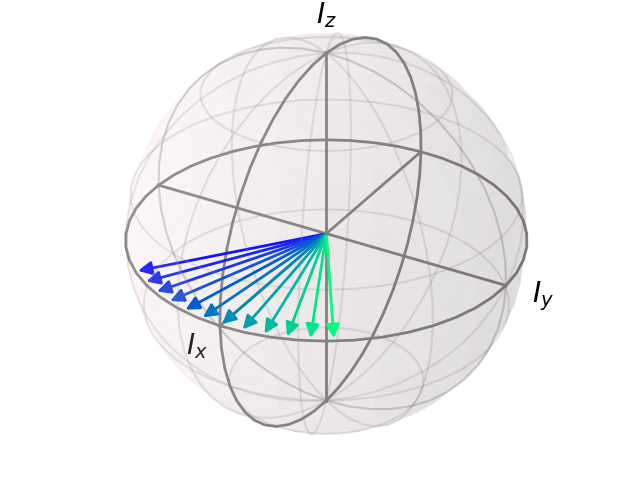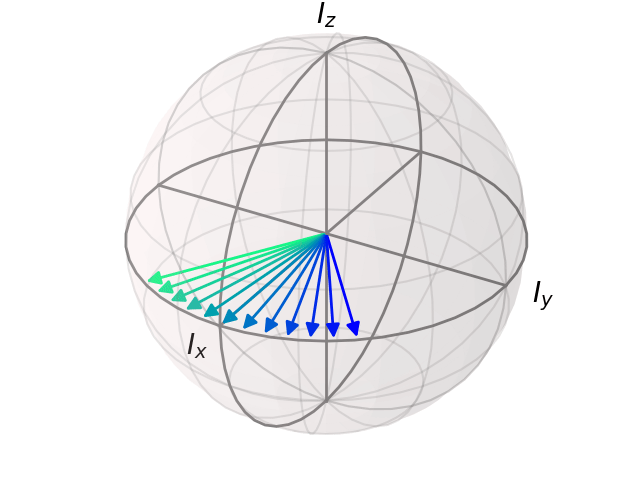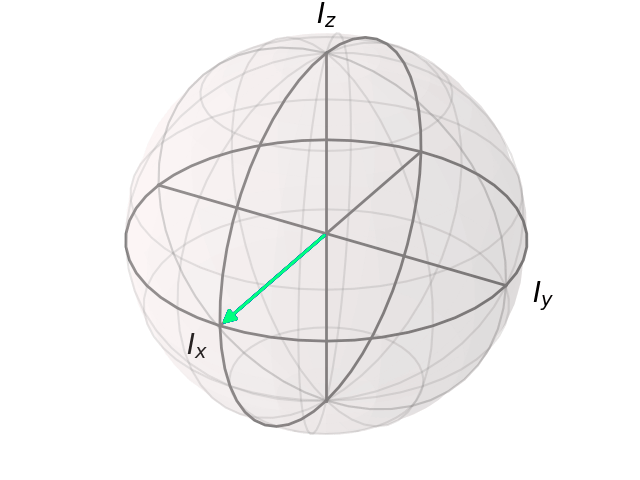
In [12]:

%%capture
bloch_animation(se_ni, spin=I, outfile='spinecho_ni.gif')

%%capture bloch_animation(se_ni, spin=I, outfile='spinecho_ni.gif')

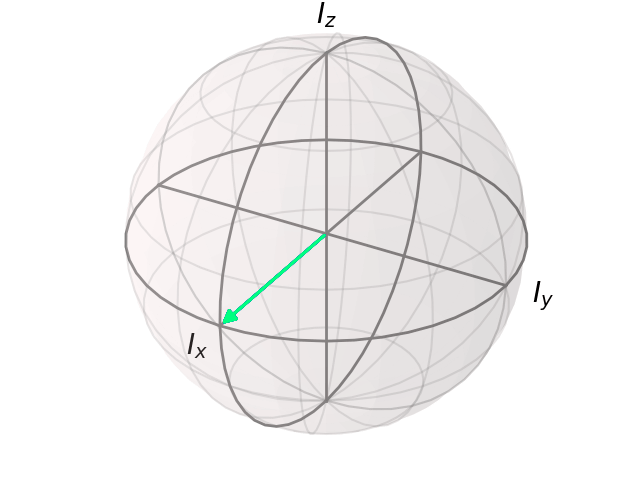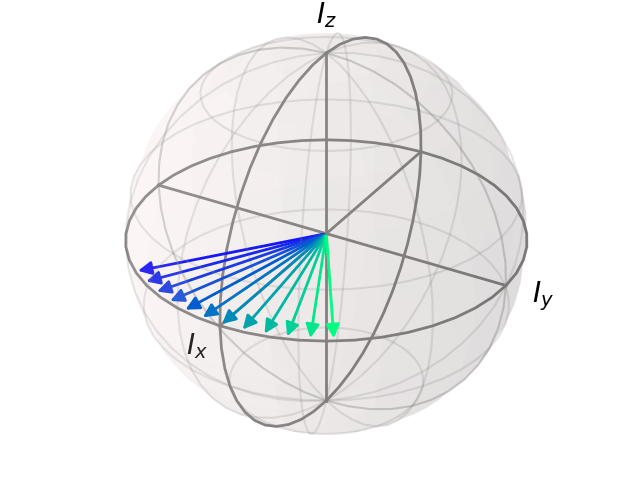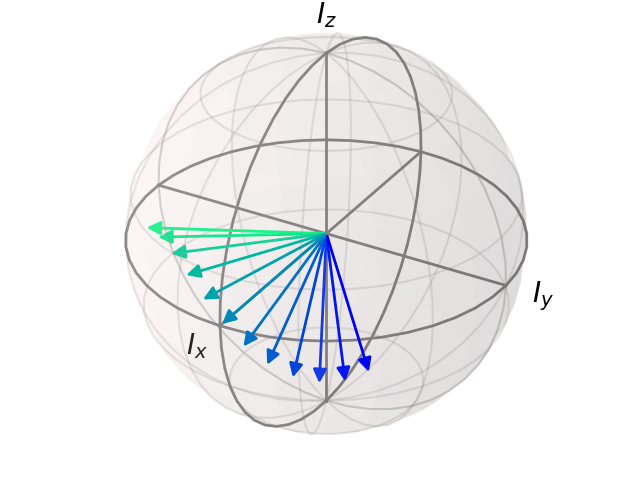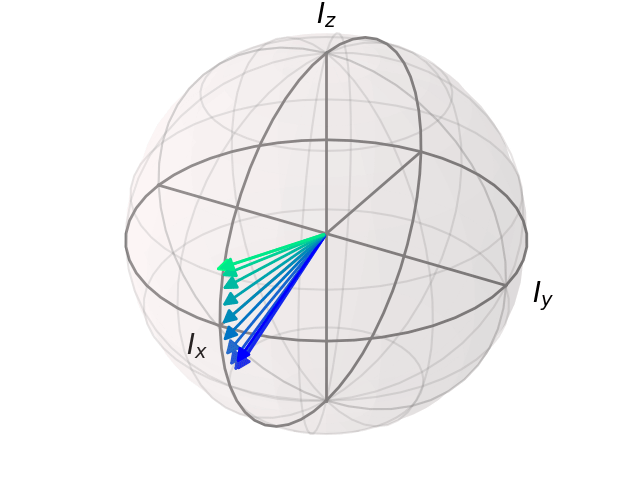
Q1¶

• Plot the intensity of the signal as a function of τ
• Plot the intensity of the signal as a function of τ for the sequence τ - pi - 2τ
• How does one understand the solid-echo using similar calculations